מתאם פירסון

מתאם פירסון ב-SPSS
מבוא
מתאם פירסון הדו-כיווני מייצר מקדם מתאם מדגם, r, אשר מודד את הכוח ואת הכיוון של יחסים לינאריים בין זוגות של משתנים מתמשכים. יתרה מזאת, מתאם פירסון מעריך האם קיימות עדויות סטטיסטיות ליחסים לינאריים בין אותם זוגות משתנים באוכלוסייה, המיוצגים על ידי מקדם מתאם אוכלוסין, ρ ("rho"). מתאם פירסון הוא מדד פרמטרי.
מדד זה ידוע גם בשם: המתאם של פירסון, מתאם פירסון למוצר-רגע.
שימושים נפוצים
מתאם הירחון הדו-חמצני משמש בדרך כלל למדידת הנקודות הבאות: מתאמים בין זוגות של משתנים מתאמים בתוך ובין קבוצות משתנים מתאם פירסון הדו-פעמי מציין את הדברים הבאים: אם קיים קשר ליניארי מובהק סטטיסטית בין שני משתנים מתמשכים כוחו של קשר ליניארי (כלומר, עד כמה קרוב הקשר להיות קו ישר לחלוטין) הכיוון של יחסים ליניאריים (הגדלה או הקטנה) הערה: הקורלציה הדו-פעמית של פירסון אינה יכולה להתייחס ליחסים לא לינאריים או ליחסים בין משתנים קטגוריים. אם ברצונכם להבין יחסים הכוללים משתנים קטגוריים ו / או יחסים לא לינאריים, יהיה עליכם לבחור מידה נוספת של אסוציאציה. הערה: מתאם פירסון הדו-כיווני מגלה רק אסוציאציות בין משתנים מתמשכים. מתאם פירסון הדו-כיווני אינו מספק שום הסקה לגבי סיבתיות, לא משנה כמה גדול מקדם המתאם הוא
דרישות נתונים
הנתונים שלך חייבים לעמוד בדרישות הבאות: שני משתנים רציפים או יותר (כלומר, מרווח או רמת יחס) מקרים שיש להם ערכים בשני המשתנים יחסים לינאריים בין המשתנים מקרים עצמאיים (כלומר עצמאות תצפיות) אין קשר בין ערכי המשתנים בין המקרים. זה אומר ש: הערכים עבור כל המשתנים בין המקרים אינם קשורים בכל מקרה, הערך עבור משתנה כלשהו אינו יכול להשפיע על הערך של משתנה כלשהו עבור מקרים אחרים אין מקרה יכול להשפיע על מקרה אחר על כל משתנה מקדם המתאם בין פירסון לבין מבחן המשמעות המקביל אינו חזק כאשר העצמאות מופרת. נורמליות דו-משתנית כל זוג של משתנים מופץ בדרך כלל באופן קבוע כל זוג של משתנים מופץ בדרך כלל באופן קבוע בכל הרמות של המשתנים האחרים (ים) הנחה זו מבטיחה כי המשתנים קשורים באופן ליניארי; הפרות של הנחה זו עשויות להצביע על יחסים לא לינאריים בין משתנים. ליניאריות ניתן להעריך ויזואלית באמצעות scatterplot של הנתונים. מדגם אקראי של נתונים מהאוכלוסייה אין חריגים
היפותזות
השערת האפס (H0) והשערה אלטרנטיבית (H1) של מבחן המשמעות של המתאם ניתנים לביטוי בדרכים הבאות, בהתאם לבדיקה של זנב אחד או שני זנב: מבחן חשיבות דו-זוויתית: H0: ρ = 0 ("מקדם המתאם של האוכלוסייה הוא 0, אין קשר") H1: ρ ≠ 0 ("מקדם המתאם של האוכלוסיה אינו 0, וקורלציה לא קיימת יכולה להתקיים") מבחן חשיבות חד-זווית: H0: ρ = 0 ("מקדם המתאם של האוכלוסייה הוא 0, אין קשר") H1: ρ> 0 ("מקדם המתאם של האוכלוסייה גדול מ -0, קשר חיובי יכול להתקיים") או H1: ρ <0 ("מקדם המתאם של האוכלוסיה הוא פחות מ -0, וקיים קשר שלילי") כאשר ρ הוא מקדם המתאם של האוכלוסייה.
הגדרת נתונים
מערך הנתונים צריך לכלול שני משתנים מספריים רציפים או יותר, כל אחד מהם מוגדר כסולם, אשר ישמשו בניתוח.
כל שורה במערך צריכה לייצג נושא ייחודי, אדם או יחידה. כל המדידות שנלקחו על אותו אדם או יחידה יופיעו בשורה זו. אם מדידות עבור נושא אחד מופיעות בשורות מרובות - לדוגמה, אם יש לך מדידות מנקודות זמן שונות בשורות נפרדות - עליך לעצב מחדש את הנתונים לפורמט "רחב" לפני חישוב המתאמים.
מדריך מתאם פירסון ב-SPSS
כדי להפעיל מתאם פירסון דו-כיווני ב- SPSS, לחץ על:
Analyze > Correlate > Bivariate
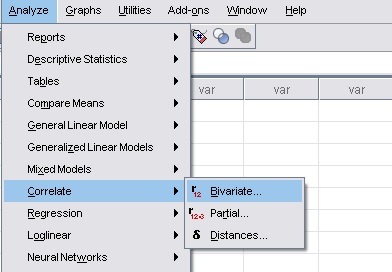
החלון Burrariate Correlations נפתח, שבו תציין את המשתנים שישמשו לניתוח. כל המשתנים במערך הנתונים מופיעים ברשימה בצד שמאל. כדי לבחור משתנים לניתוח, בחר את המשתנים ברשימה שמשמאל ולחץ על לחצן החץ הכחול כדי להזיז אותם ימינה, בשדה המשתנים.
המשתנים: המשתנים שישמשו בקורלציית הירחון הדו-כיווני. עליך לבחור לפחות שני משתנים רציפים, אך ניתן לבחור יותר משניים. הבדיקה תייצר מקדמי קורלציה עבור כל זוג משתנים ברשימה זו. מקדמי המתאם: קיימים מספר סוגים של מקדמי קורלציה. כברירת מחדל, Pearson נבחר. בחירת Pearson תייצר את הנתונים הסטטיסטיים של הבדיקה עבור מתאם פירסון bivariate. מבחן המשמעות: לחץ על שני זנב או זנב אחד, בהתאם למבחן המשמעות הרצוי שלך. SPSS משתמש בבדיקה דו-זוויתית כברירת מחדל. סמן קורלציות משמעותיות: בדיקת אפשרות זו תכלול כוכביות (**) ליד מתאם משמעותי סטטיסטית בפלט. כברירת מחדל, SPSS מסמן מובהקות סטטיסטית ברמות אלפא = 0.05 ואלפא = 0.01, אך לא ברמת אלפא = 0.001 (אשר מטופלת כ- 0.01 אלפא) אפשרויות: לחיצה על אפשרויות תפתח חלון שבו תוכל לציין אילו נתונים סטטיסטיים יכללו (כלומר, אמצעים וסטיות תקן, סטיות בין מוצרים וחלוקות) וכיצד לטפל בערכים חסרים (כלומר, אל תכלול מקרים בהתאמה זוגית או אל תכלול מקרים). שים לב שהגדרת ה- pairwise / listwise אינה משפיעה על החישובים שלך אם אתה מזין רק שני משתנים, אבל יכול לעשות הבדל גדול מאוד אם אתה מזין שלושה משתנים או יותר בהליך המתאם.
דוגמה: הבנת הקשר הליניארי בין משקל לגובה
הצהרה על הבעיה
ייתכן שתרצה לבדוק האם קיים קשר ליניארי מובהק סטטיסטית בין שני משתנים רציפים, משקל וגובה (ובהתאם לכך ניתן להסיק אם הקשר משמעותי באוכלוסייה). ניתן להשתמש בקורלציה דו-כיוונית דו-כיוונית לבדיקת האם יש קשר ליניארי מובהק סטטיסטית בין גובה ומשקל, וכדי לקבוע את חוזק וכיוון העמותה.
לפני הבדיקה ב-spss
בנתוני המדגם נשתמש בשני משתנים: "גובה" ו "משקל". המשתנה "גובה" הוא מדד רציף של גובה מילימטרים ובתערוכות טווח של ערכים מ -155 ל -195 המשתנה "משקל" הוא מדד רציף של משקל בקילוגרמים ומוצגים טווח של ערכים מ 48 ל-115 כדי לבדוק זאת במהירות בתוכנת SPSS לחצו על:
Analyze > DescriptiveStatistics > Descriptives
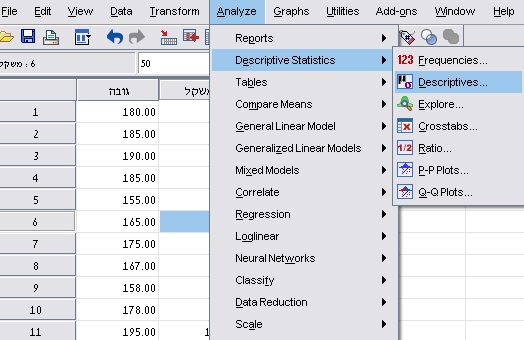
מכניסים משתנים גובה ומשקל לצד ימין כפי שרואים בתמונה
ומקבלים פלט הבא, אשר מתאר נתוני מינימום, מקסימום, ממוצע וסטיית תקן של המשתנים גובה ומשקל במקרה שלנו.
לפני שאנחנו מסתכלים על המתאמים של פירסון, אנחנו צריכים להסתכל על scatterplots של המשתנים שלנו כדי לקבל מושג מה לצפות. בפרט, עלינו לקבוע אם סביר להניח שלמשתנים שלנו יש יחסים לינאריים. לחץ על:
Graphs > Legacy Dialogs > Scatter/Dot --> Simple Scatter --> Define
העבר משתנה גובה אל תיבת ציר X, והעבר משתנה משקל לתיבה ציר Y. בסיום, לחץ על אישור (OK)
כדי להוסיף התאמה ליניארית כמו זו המתוארת, לחץ לחיצה כפולה על העלילה ב Output Viewer כדי לפתוח את עורך התרשימים. לחץ על:
Elements > Fit Line at Total
בחלון Properties יש לוודא כי Fit Method מוגדר לינארי (Linear) ולאחר מכן לחצו Apply
מן scatterplot, אנו יכולים לראות כי ככל גובה מגדילה, משקל גם נוטה להגדיל. נראה שיש כמה יחסים ליניארי.
המבחן
כדי להפעיל את מתאם Pearson הדו-שנתי, לחץ על Analyze > Correlate > Bivariate בחר את המשתנים גובה ומשקל והעבר אותם לתיבה 'משתנים'. בתוך ה-Correlation Coefficients מסומן Pearson. ב- Test of Significance אזור, בחר את מבחן המשמעות הרצוי, שני זנבות או זנב אחד. אנו בוחרים במבחן משמעות דו-זנב בדוגמה זו. סמן את התיבה שלצד Flag significant correlations. לאחר מכן לחצו OK.
פלט SPSS מתאם פירסון
התוצאות יציגו את המתאמים בטבלה, שכותרתו קורלציות.
קורלציה של גובה ומשקל (r = 0.943), המבוססת על n = 11 תצפיות.
החלטה ומסקנות
בהתבסס על התוצאות, אנו יכולים לציין את הדברים הבאים: • משקל וגובה יש קשר ליניארי מובהק סטטיסטית (p <.001). • כיוון הקשר הוא חיובי (כלומר, גובה ומשקל מתואמים באופן חיובי), כלומר משתנים אלו נוטים לגדול יחד (כלומר, גובה גדול יותר קשור למשקל גדול יותר). • הגודל, או העוצמה, של העמותה הוא מתון בערך (0.3 <| r | <5).
{ניתוח סטטיסטי}
















