ניתוח שונות חד כיווני

One-way ANOVA - ניתוח שונות חד כיווני - SPSS

מבוא

ניתוח השונות החד-כיווני (ANOVA) משמש כדי לקבוע אם יש הבדלים מובהקים סטטיסטית בין האמצעים של שתי קבוצות או יותר עצמאיות (לא קשורות) (למרות שאתה נוטה לראות את השימוש בהן רק כשיש מינימום שלוש, ולא שתי קבוצות). לדוגמה, אתה יכול להשתמש ב- ANOVA חד כיווני כדי להבין אם ביצועי הבחינה שונים על סמך רמות חרדת מבחנים בקרב סטודנטים, וחלוקת סטודנטים לשלוש קבוצות עצמאיות (למשל, סטודנטים נמוכים, בינוניים וגבוהים בלחץ). כמו כן, חשוב להבין כי ה- ANOVA החד-כיווני הוא נתון של מבחן אומניבוס ואינו יכול לומר לך אילו קבוצות ספציפיות היו שונות באופן סטטיסטי זו מזו; זה רק אומר לך שלפחות שתי קבוצות היו שונות זו מזו. מכיוון שיש לך שלוש, ארבע, חמש או יותר קבוצות בעיצוב המחקר שלך, חשוב לקבוע אילו מהקבוצות הללו שונות זו מזו. אתה יכול לעשות זאת באמצעות מבחן פוסט הוק (N.B., אנו דנים בבדיקות פוסט הוק בהמשך מדריך זה).

מדריך "התחלה מהירה" זו מראה לך כיצד לבצע ANOVA חד כיווני באמצעות סטטיסטיקה של SPSS, כמו גם לפרש ולדווח על התוצאות ממבחן זה. מכיוון שלעתים קרובות מעקב אחר ה- ANOVA החד-כיווני במבחן פוסט-הוק, אנו גם מראים לכם כיצד לבצע מבחן פוסט-הוק באמצעות סטטיסטיקה של SPSS. עם זאת, לפני שנכיר לכם את הנוהל הזה, עליכם להבין את ההנחות השונות שעומדות בנתונים שלכם כדי לעמוד בכדי ש- ANOVA חד-כיווני תביא לכם תוצאה תקפה. בהמשך נדון בהנחות אלה.

הנחות

כשאתה בוחר לנתח את הנתונים שלך באמצעות ANOVA חד כיווני , חלק מהתהליך כרוך בבדיקה כדי לוודא שניתן למעשה לנתח את הנתונים שאתה רוצה לנתח באמצעות ANOVA חד כיווני . עליכם לעשות זאת מכיוון שנכון להשתמש רק ב- ANOVA חד כיווני אם הנתונים שלכם “עוברים” שש הנחות הנדרשות כדי ש- ANOVA חד-כיווני תביא לכם תוצאה תקפה. בפועל, בדיקת שש ההנחות הללו רק מוסיפה קצת יותר זמן לניתוח שלך, ומחייבת לך ללחוץ על עוד כמה כפתורים בסטטיסטיקה של SPSS בעת ביצוע הניתוח שלך, כמו גם לחשוב קצת יותר על הנתונים שלך, אבל זה משימה לא קשה.

לפני שנכיר לך את שש ההנחות הללו, אל תתפלא אם בניתוח הנתונים שלך בעצמך תוך שימוש בסטטיסטיקה של SPSS, הפרה אחת או יותר מההנחות הללו (כלומר, לא מתקיימת). זה לא נדיר כאשר עובדים עם נתונים בעולם האמיתי ולא עם דוגמאות לספרי לימוד, שלרוב רק מראים לכם כיצד לבצע ANOVA חד כיווני כשהכל מסתדר! עם זאת, אל תדאג. גם כאשר הנתונים שלך נכשלים בהנחות מסוימות, לרוב יש פיתרון להתגבר על זה. ראשית, נסתכל על שש ההנחות הללו:

הנחה מספר 1
יש למדוד את שני המשתנים שלך ברמה הרציפה (כלומר, הם משתני מרווח או יחס). דוגמאות למשתנים רציפים כוללים זמן עדכון (נמדד בשעות), אינטליגנציה (נמדדת באמצעות ציון מנת משכל), ביצועי הבחינה (נמדד מ -0 ל -100), משקל (נמדד בק"ג) וכן הלאה.

הנחה מספר 2
המשתנה הבלתי תלוי שלך צריך להיות מורכב משתי קבוצות או יותר קטגוריות עצמאיות. בדרך כלל, ANOVA חד כיווני משמשת כשיש לך שלוש קבוצות או פחות קטגוריות עצמאיות, אך ניתן להשתמש בה לשתי קבוצות בלבד (אך מבחן t- דוגמא עצמאי משמש יותר לשתי קבוצות). דוגמא למשתנים עצמאיים העומדים בקריטריון זה כוללים אתניות (למשל, 3 קבוצות: קווקזית, אמריקה אפריקאית והיספנית), רמת פעילות גופנית (למשל, 4 קבוצות: מושב, נמוך, בינוני וגבוה), מקצוע (למשל, 5 קבוצות: מנתח, רופא, אחות, רופא שיניים, מטפל) וכן הלאה.

הנחה מספר 3
עליכם להיות עצמאים של תצפיות, מה שאומר שאין קשר בין התצפיות בכל קבוצה או בין הקבוצות עצמן. לדוגמה, חייבים להיות משתתפים שונים בכל קבוצה, כאשר אף משתתף אינו נמצא בקבוצה אחת יותר. זה יותר נושא העיצוב המחקר מאשר משהו שאתה יכול לבדוק עבורו, אבל זו הנחה חשובה של ה- ANOVA החד-כיווני . אם המחקר שלך נכשל בהנחה זו, תצטרך להשתמש במבחן סטטיסטי אחר במקום ה- ניתוח שונות החד-כיווני (למשל, עיצוב מודד חוזר ונשנה). אם אינך בטוח אם המחקר שלך עומד בהנחה זו, אתה יכול להשתמש בבורר הבדיקה הסטטיסטי שלנו, שהוא חלק מהמדריכים המשופרים שלנו.

הנחה מספר 4
לא אמורים להיות חריגים משמעותיים. מחיצות הן פשוט נקודות נתונים בודדות בתוך הנתונים שלך שאינן עוקבות אחר התבנית הרגילה (למשל, במחקר שנערך על 100 ציוני מנת המשכל של התלמידים, שם הציון הממוצע היה 108 עם וריאציה קטנה בלבד בין התלמידים, סטודנט אחד היה ציון של 156 , וזה מאוד יוצא דופן, ואף עשוי להכניס אותה ל -1% המובילים של ציוני ה- IQ ברחבי העולם. הבעיה עם המממנים היא שהם יכולים להשפיע לרעה על ה- ANOVA החד-כיווני, ולהפחית את תוקף התוצאות שלך. למרבה המזל, כשאתה משתמש בסטטיסטיקה של SPSS להפעלת ANOVA חד כיווני על הנתונים שלך, אתה יכול לאתר בקלות מחיצות אפשריות. במדריך ה- ניתוח שונות החד-כיווני המשופר שלנו, אנו: (א) מראים לך כיצד לאתר מחיצות באמצעות סטטיסטיקה של SPSS; ו (ב) לדון בכמה מהאפשרויות העומדות בפניך כדי להתמודד עם מתחרים. תוכל ללמוד עוד על מדריך ה- ANOVA החד-כיוון המשופר שלנו על התכונות שלנו: דף ניתוח שונות חד כיווני.

הנחה מספר 5
המשתנה התלוי צריך להיות מופץ באופן רגיל לכל קטגוריה של המשתנה הבלתי תלוי. אנו מדברים על ANOVA חד כיווני הדורשת רק נתונים רגילים בערך מכיוון שהיא די "איתנה" להפרות הנורמליות, כלומר ניתן להפר מעט את ההנחה ועדיין לספק תוצאות תקפות. אתה יכול לבדוק נורמליות באמצעות מבחן Shapiro-Wilk לנורמליות, אשר נבדק בקלות על ידי שימוש בסטטיסטיקה של SPSS. בנוסף להראות לך כיצד לעשות זאת במדריך ה- ANOVA החד-משופר שלנו, אנו גם מסבירים מה אתה יכול לעשות אם הנתונים שלך נכשלים בהנחה זו (כלומר אם הם נכשלים בהם יותר מקצת). שוב, תוכלו ללמוד עוד על התכונות שלנו: דף ANOVA חד כיווני.

הנחה מספר 6
צריכה להיות הומוגניות של שונות. אתה יכול לבדוק הנחה זו בסטטיסטיקה של SPSS באמצעות המבחן של Levene להומוגניות של שונות. אם הנתונים שלך נכשלים בהנחה זו, תצטרך לא רק לבצע Welch ANOVA במקום ANOVA חד כיווני, שתוכל לעשות באמצעות SPSS Statistics, אלא גם להשתמש במבחן פוסט הוק אחר. במדריך ה- ANOVA החד-כיווני המשופר שלנו, אנו (א) מראים לכם כיצד לבצע את מבחן Levene לבחינת הומוגניות של שונות בסטטיסטיקה של SPSS, (ב) להסביר כמה מהדברים שתצטרכו לקחת בחשבון בעת פרשנות הנתונים שלכם, ו- (c) להציג דרכים אפשריות להמשיך בניתוח שלך אם הנתונים שלך לא עומדים בהנחה זו, כולל הפעלת Welch ANOVA בסטטיסטיקה של SPSS במקום מבחן ANOVA חד כיווני, ובדיקת Games-Howell במקום מבחן Tukey פוסט הוק (למידע נוסף על התכונות שלנו: דף ANOVA לכיוון).

אתה יכול לבדוק את ההנחות # 4, # 5 ו- # 6 באמצעות נתונים סטטיסטיים של SPSS. לפני שתעשה זאת, עליך לוודא שהנתונים שלך עומדים בהנחות מס '1, # 2 ו- # 3, אם כי אינך זקוק לסטטיסטיקה של SPSS כדי לעשות זאת. זכור שאם לא תריץ נכון את הבדיקות הסטטיסטיות בהנחות אלה, יתכן שהתוצאות שתקבל בעת הפעלת ANOVA חד כיווני אינן תקפות. זו הסיבה שאנו מקדישים מספר קטעים ממדריך ה- ANOVA החד-כיווני המשופר שלנו כדי לעזור לך להשיג זאת נכון. תוכל לברר אודות מדריך ה- ANOVA החד-כיווני המשופר שלנו על התכונות שלנו: דף ANOVA חד כיווני, או באופן כללי יותר, התוכן המשופר שלנו בכללותו בדף התכונות שלנו: סקירה כללית.

איך מריצים One-way ANOVA - ניתוח שונות חד כיווני ב-SPSS

לצורך הדוגמה והתרגות הורידו את הקובץ הבא:
קובץ תרגול להורדה

בקובץ קיימים נתונים דמוגרפים רבים שיעזרו לנו לעשות ניתוחים סטטיסטיים שונים,
נתמקד כרגע בהרצת One-way ANOVA - ניתוח שונות חד כיווני

מדריך חמשת השלבים One-way ANOVA - ניתוח שונות חד כיווני ב-SPSS

לצורך דוגמה נקח משתנים הבאים: משתנה בלתי תלוי (מסביר) תעודה, ומשתנה רציף - שכר עבודה משתנה תלוי (מוסבר)

הורידו קובץ לדוגמה ופתחו אותו בתוכנת SPSS

Analyze > Compare Means > One-Way ANOVA

בחלון שיפתח בחרו משתנה תלוי שכר עבודה - inc93
ומשתנה בלתי תלוי - diploma
והכניסו אותם אחד אחד בעזרת כפתור:

לאחר בחירת המשתנים יש ללחוצ על כפתור סמנו - ולחצו

לאחר מכן לחצו על כפתור - בחרו- ולחצו

לאחר מכן לחצו על כפתור -

הסבר של פלט SPSS - One-way ANOVA - ניתוח שונות חד כיווני

לוח סטטיסטיקה תיאורים

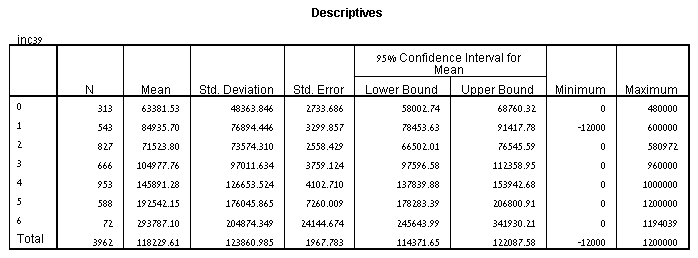
טבלת התיאורים (ראה להלן) מספקת נתונים סטטיסטיים תיאוריים שימושיים מאוד, כולל הממוצע, סטיית התקן ומרווחי ביטחון של 95% עבור המשתנה התלוי (inc39) עבור כל קבוצה נפרדת של משתנה עצמאי (תעודה), כמו גם כאשר כל הקבוצות הן משולב (סה"כ). נתונים אלה מועילים כאשר עליך לתאר את הנתונים שלך.

טבלת ANOVA

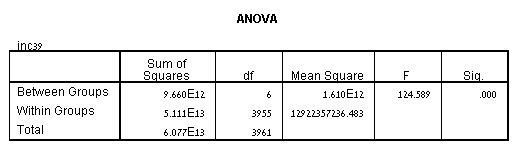
זה הטבלה שמציגה את תפוקת ניתוח ANOVA והאם יש הבדל מובהק סטטיסטית בין אמצעי הקבוצה שלנו. אנו יכולים לראות שערך המשמעות הוא 0.000 (כלומר, p = .000), הנמצא מתחת ל- 0.05. ולכן יש הבדל מובהק סטטיסטית במשך הזמן הממוצע להשלמת בעיית הגיליון האלקטרוני בין הקורסים השונים שנלקחו. זה נהדר לדעת, אך איננו יודעים איזו מהקבוצות הספציפיות נבדלות זו מזו. למזלנו, אנו יכולים לגלות זאת בטבלת ההשוואות המרובות המכילות את תוצאות מבחן ה- Tukey שלאחר ההוק.

טבלט Post Hoc

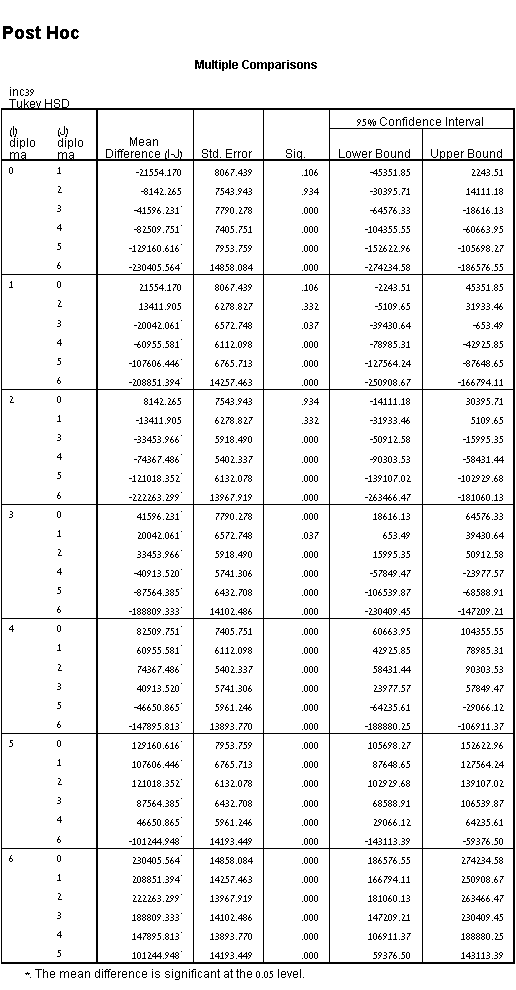
מהתוצאות עד כה אנו יודעים שיש הבדלים מובהקים סטטיסטית בין הקבוצות בכללותן. הטבלה שלהלן, מספר השוואות, מראה אילו קבוצות שונות זו מזו. מבחן הטוקי פוסט-הוק הוא בדרך כלל המבחן המועדף על ביצוע בדיקות פוסט-הוק במבחן ANOVA חד כיווני, אך ישנם רבים אחרים. אנו יכולים לראות מהטבלה שלהלן כי קיים הבדל משמעותי סטטיסטית בזמן להשלמת הבעיה בין הקבוצה (p = 0.000 או p <0.05) עם זאת, לא היו הבדלים בין הקבוצות (p> 0.05).

{ניתוח סטטיסטי}