ניתוח שונות דו כיווני

Two way ANOVA - ניתוח שונות דו כיווני - SPSS

מהו ניתוח שונות דו כיווני?

מבחן ANOVA דו כיווני הוא מבחן סטטיסטי המשמש לקביעת ההשפעה של שני משתני חיזוי נומינליים על משתנה תוצאות רציף. ANOVA מייצג ניתוח של שונות ובדיקות להבדלים בהשפעות של משתנים עצמאיים על משתנה תלוי.

ANOVA דו כיווני בודק את ההשפעה של שני משתנים עצמאיים על משתנה תלוי. מבחן ANOVA דו כיווני מנתח את השפעת המשתנים הבלתי תלויים על התוצאה הצפויה יחד עם הקשר שלהם לתוצאה עצמה. גורמים אקראיים ייחשבו כבעלי שום השפעה סטטיסטית על מערך הנתונים, ואילו גורמים שיטתיים ייחשבו כבעלי משמעות סטטיסטית.

על ידי שימוש ב- ANOVA, חוקר מסוגל לקבוע אם השתנות התוצאות נובעת מקריות או מהגורמים בניתוח. ל- ANOVA יישומים רבים בתחומי מימון, כלכלה, מדע, רפואה ומדעי החברה.

היסודות של ANOVA דו כיוונית

מבחן ANOVA הוא הצעד הראשון בזיהוי גורמים המשפיעים על תוצאה נתונה. לאחר ביצוע בדיקת ANOVA, בודק עשוי להיות מסוגל לבצע ניתוח נוסף על הגורמים השיטתיים התורמים סטטיסטית לשונות מערך הנתונים. מבחן ANOVA דו כיווני חושף את התוצאות של שני משתנים עצמאיים על משתנה תלוי. לאחר מכן ניתן להשתמש בתוצאות בדיקת ANOVA במבחן F על המשמעות של נוסחת הרגרסיה באופן כללי.

ניתוח השונות מועיל לבדיקת השפעות המשתנים זה על זה. זה דומה לבדיקות t דו-מדגמיות מרובות. עם זאת, התוצאה היא פחות שגיאות מסוג 1 ומתאימה למגוון בעיות. ANOVA מקבצת הבדלים על ידי השוואה בין האמצעים של כל קבוצה וכוללת הפצת השונות למקורות מגוונים. זה מועסק עם נבדקים, קבוצות מבחן, בין קבוצות ותוך קבוצות.

נקודות חשובות

ANOVA דו כיוונית היא הרחבה של ANOVA חד כיוונית (ניתוח שונות) החושף את התוצאות של שני משתנים עצמאיים על משתנה תלוי.

מבחן ANOVA דו כיווני הוא טכניקה סטטיסטית המנתחת את השפעת המשתנים הבלתי תלויים על התוצאה הצפויה יחד עם הקשר שלהם לתוצאה עצמה.

ל- ANOVA יישומים רבים בתחום הפיננסים והכלכלה, מדע, רפואה ומדעי החברה.

הנחה מספר 1
יש למדוד את המשתנה התלוי שלך ברציפות (כלומר, הם משתני מרווח או יחס). דוגמאות למשתנים רציפים כוללים זמן עדכון (נמדד בשעות), אינטליגנציה (נמדדת באמצעות ציון מנת משכל), ביצועי הבחינה (נמדד מ -0 ל -100), משקל (נמדד בק"ג) וכן הלאה. תוכלו ללמוד עוד על משתני מרווח ויחס במאמר שלנו: סוגי משתנים.

הנחה מספר 2
שני המשתנים הבלתי תלויים צריכים להיות מורכבים משתי קבוצות או יותר קטגוריות עצמאיות. דוגמא למשתנים עצמאיים העומדים בקריטריון זה כוללים מגדר (2 קבוצות: זכר או נקבה), אתניות (3 קבוצות: קווקזי, אפרו-אמריקני והיספני), מקצוע (5 קבוצות: מנתח, רופא, אחות, רופא שיניים, מטפל) וכדומה. .

הנחה מספר 3
עליכם להיות עצמאים של תצפיות, מה שאומר שאין קשר בין התצפיות בכל קבוצה או בין הקבוצות עצמן. לדוגמה, חייבים להיות משתתפים שונים בכל קבוצה, כאשר אף משתתף אינו נמצא בקבוצה אחת יותר. זה יותר נושא העיצוב של המחקר מאשר משהו שהיית בודק עבורו, אבל זו הנחה חשובה של ה- ANOVA הדו כיוונית. אם המחקר שלך נכשל בהנחה זו, תצטרך להשתמש במבחן סטטיסטי אחר במקום ה- ANOVA הדו-כיווני (למשל, תכנון מדוד חוזר ונשנה). אם אינך בטוח אם המחקר שלך עומד בהנחה זו, אתה יכול להשתמש בבורר הבדיקה הסטטיסטי שלנו, שהוא חלק מהמדריכים המשופרים שלנו.

הנחה מספר 4
לא אמורים להיות חריגים משמעותיים. מחיצות הן נקודות נתונים בתוך הנתונים שלך שאינן עוקבות אחר הדפוס הרגיל (למשל, במחקר שערך 100 ציוני מנת המשכל של התלמידים, שם הציון הממוצע היה 108 עם שונות קטנה בלבד בין התלמידים, סטודנט אחד היה ציון של 156, אשר זה מאוד יוצא דופן, ואף עשוי להכניס אותה ל -1% המובילים של ציוני ה- IQ ברחבי העולם. הבעיה עם הממדים היא שהם יכולים להשפיע לרעה על ה- ANOVA הדו כיוונית, ולהפחית את הדיוק של התוצאות שלך. למרבה המזל, כשאתה משתמש בסטטיסטיקה של SPSS להפעלת ANOVA דו כיוונית על הנתונים שלך, אתה יכול לאתר בקלות מחיצות אפשריות. במדריך ANOVA הדו-כיווני המשופר שלנו, אנו: (א) מראים לך כיצד לזהות מחיצים באמצעות סטטיסטיקה של SPSS; ו (ב) לדון בכמה מהאפשרויות העומדות בפניך כדי להתמודד עם מתחרים.

הנחה מספר 5
המשתנה התלוי צריך להיות מופץ באופן רגיל לכל שילוב של הקבוצות של שני המשתנים הבלתי תלויים. אמנם זה נשמע מעט מסובך, אך הוא נבדק בקלות לשימוש בסטטיסטיקה של SPSS. כמו כן, כאשר אנו מדברים על ANOVA דו כיוונית הדורשת רק נתונים נורמליים בערך, הסיבה לכך היא שהיא די "איתנה" להפרות נורמליות, כלומר ההנחה יכולה להיות מופרת מעט ועדיין לספק תוצאות תקפות. ניתן לבדוק נורמליות באמצעות מבחן Shapiro-Wilk לנורמליות, אשר נבדק בקלות על ידי שימוש בסטטיסטיקה של SPSS. בנוסף להראות לך כיצד לעשות זאת במדריך ANOVA הדו-כיווני המשופר שלנו, אנו גם מסבירים מה אתה יכול לעשות אם הנתונים שלך נכשלים בהנחה זו (כלומר אם הם נכשלים בהם יותר מקצת).

הנחה מספר 6
צריכה להיות הומוגניות של שונות עבור כל שילוב של הקבוצות של שני המשתנים הבלתי תלויים. שוב, למרות שזה נשמע מעט מסובך, אתה יכול בקלות לבדוק את ההנחה הזו בסטטיסטיקה של SPSS באמצעות המבחן של Levene להומוגניות של שונות. במדריך ה- ANOVA הדו-כיווני המשופר שלנו, אנו (א) מראים לכם כיצד לבצע את מבחן Levene לבחינת הומוגניות של שונות בסטטיסטיקה של SPSS, (ב) להסביר כמה מהדברים שתצטרכו לקחת בחשבון בעת פרשנות הנתונים שלכם, ו- (c) הציג דרכים אפשריות להמשיך בניתוח שלך אם הנתונים שלך לא עומדים בהנחה זו.

אתה יכול לבדוק את ההנחות # 4, # 5 ו- # 6 באמצעות נתונים סטטיסטיים של SPSS. לפני שתעשה זאת, עליך לוודא שהנתונים שלך עומדים בהנחות מס '1, # 2 ו- 3, אם כי אינך זקוק לסטטיסטיקה של SPSS כדי לעשות זאת. רק זכרו שאם לא תריצו נכון את המבחנים הסטטיסטיים בהנחות אלה, יתכן שהתוצאות שתקבלו בעת הפעלת ANOVA דו כיוונית אינן תקפות. זו הסיבה שאנו מקדישים מספר חלקים במדריך ה- ANOVA המשופך שלנו בכדי לעזור לכם להשיג זאת נכון. תוכל לגלות על התוכן המשופר שלנו בכללותו בדף התכונות שלנו: סקירה כללית, או ליתר דיוק, ללמוד כיצד אנו עוזרים בבדיקת הנחות בדף התכונות שלנו: הנחות.

ניתוח שונות דו כיווני (Two-Way ANOVA) ב-SPSS

לצורך הדוגמה והתרגות הורידו את הקובץ הבא:
קובץ תרגול להורדה

בקובץ קיימים נתונים דמוגרפים רבים שיעזרו לנו לעשות ניתוחים סטטיסטיים שונים,
נתמקד כרגע בהרצת ניתוח שונות דו כיווני (Two-Way ANOVA) ב-SPSS

מדריך שלב אחר שלב Two-way ANOVA - ניתוח שונות חד כיוונית ב-SPSS

לצורך דוגמה נקח משתנים הבאים:
משתנה תלוי - שעות עבודה שבועיות
ומשתנים בלתי תלויים - מין ותעודה

הורידו קובץ לדוגמה ופתחו אותו בתוכנת SPSS

לחצו על Analyze > General Linear Model > Univariate כפי שמופיע בתמונה

תוצג בפניך תיבה Univariate, כמוצג להלן:

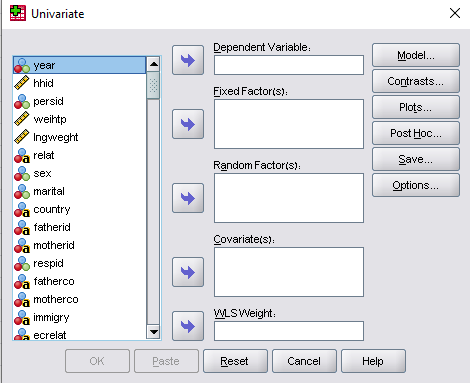
העבר את המשתנה התלוי, שעות עבודה, לתיבה משתנה תלוי: והעביר את שני המשתנים הבלתי תלויים, מגדר ותעודה, לתיבה הגורמים הקבועים:. תוכלו לעשות זאת על ידי גרירה ושחרור של המשתנים לתיבות המתאימות או באמצעות כפתור החץ ימינה . אם אתה משתמש בגרסאות ישנות יותר של סטטיסטיקה של SPSS, תצטרך להשתמש בשיטה האחרונה. בסופו של דבר עם מסך דומה לזה שמוצג להלן:

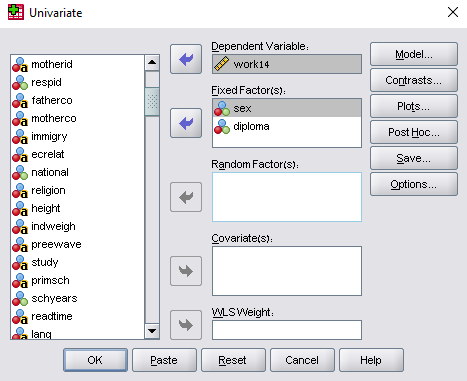
לחצו על

תוצג בפניך תיבת הדו-שיח Univariate: Profil Plots, כמוצג להלן:

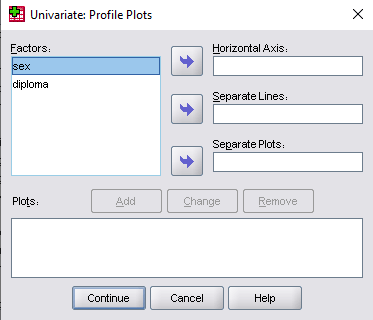
הכניסו משתנה diploma ב-Horizontal Axis, משתנה sex ב-Separate Lines בעזרת כפתור לאחר מכן לחצו Add ולבסוף

לחצו על תוצג בפניך: Univariate: Post Hoc Multiple Comparisons for Observed Means כפי שניתן לראות בתמונה הבאה :

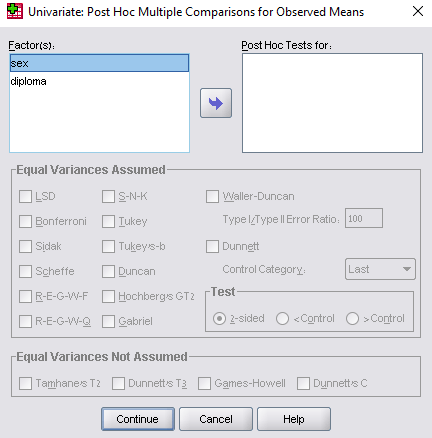
הכניסו משתנה diploma לחצו ולאחר מכן לחצו על

לחצו על הניסו את כל המשתנים כפי שמופיע בתמונה סמנו - ולחצו

ולבסוף לחצו

פלט סטטיסטי של SPSS - ניתוח שונות דו כיווני

סטטיסטיקה של SPSS מייצרת לא מעט טבלאות בתפוקה שלה מ- ANOVA דו כיוונית. בחלק זה אנו מראים לך את הטבלאות העיקריות הנדרשות להבנת התוצאות שלך מ- ANOVA דו כיוונית, כולל תיאורים, השפעות בין נושאים, מבחני פוסט-הוק טוקי (השוואה מרובה), עלילת התוצאות ואיך לרשום תוצאות אלה.

להסבר מלא על התפוקה שעליך לפרש בבדיקת הנתונים שלך לגבי שש ההנחות הדרושות לביצוע ANOVA דו כיווני, עיין במדריך המשופר שלנו. זה כולל מגרשי קופסא רלוונטיים, ופלט ממבחן שפירו-וילק שלך לנורמליות ובדיקה להומוגניות של שונות.

לבסוף, אם יש לך אינטראקציה משמעותית סטטיסטית, תצטרך לדווח גם על השפעות עיקריות פשוטות. לחילופין, אם אין לך אינטראקציה משמעותית סטטיסטית, ישנם נהלים אחרים שתצטרך לבצע. אנו מראים לך נהלים אלה בסטטיסטיקה של SPSS, וכן כיצד לפרש ולכתוב את התוצאות שלך במדריך ANOVA הדו-כיווני המשופר.

סטטיסטיקה תיאורית

אתה יכול למצוא נתונים סטטיסטיים תיאוריים המתאימים כאשר אתה מדווח על תוצאות ה- ANOVA הדו-כיוונית בטבלה המכונה "סטטיסטיקה תיאורית", כמתואר להלן:

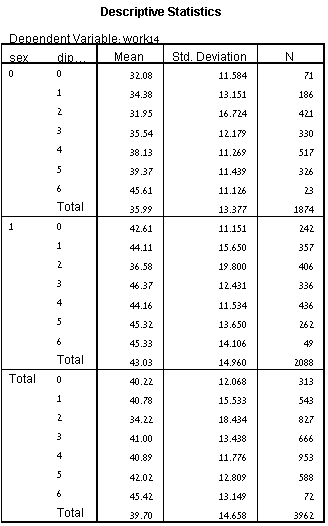
טבלה זו שימושית מאוד מכיוון שהיא מספקת את הממוצע וסטיית התקן עבור כל שילוב של קבוצות המשתנים הבלתי תלויים (מה שמכונה לעיתים כל "תא" של העיצוב). בנוסף, הטבלה מספקת שורות "סה"כ", המאפשרות אמצעים וסטיות תקן לקבוצות המפוצלות רק על ידי משתנה עצמאי אחד, או בכלל לא, ידוע. זה עשוי להיות שימושי יותר אם אין לך אינטראקציה משמעותית סטטיסטית.

גרף עם התוצאות

העלילה של ציון "מעשי העבודה" הממוצע עבור כל שילוב של קבוצות "מין" ו"דיפלומה "מתוארים בתרשים שורות, כמוצג להלן:

למרות שגרף זה ככל הנראה אינו איכותי מספיק בכדי להציג בדוחות שלך (אתה יכול לערוך את המראה שלו בסטטיסטיקה של SPSS), הוא נוטה לספק המחשה גרפית טובה של התוצאות שלך. בדרך כלל ניתן לראות אפקט אינטראקציה כסט קווים לא מקבילים. ניתן לראות מגרף זה כי נראה כי הקווים אינם מקבילים (כאשר הקווים עוברים למעשה). ניתן לצפות שיהיה אינטראקציה משמעותית סטטיסטית, אותה אנו יכולים לאשר בסעיף הבא.

המשמעות הסטטיסטית של ה- ניתוח שונות דו כיווני

התוצאה בפועל של ניתוח שונות דו כיווני - כלומר אם אחד משני המשתנים העצמאיים או האינטראקציה ביניהם הם בעלי משמעות סטטיסטית - מוצגת בטבלת הבדיקות של אפקטים בין נושאים, כמוצג להלן:

השורות הספציפיות בהן אנו מעוניינים הן שורות "מין", "תעודה" ו"סקס * תעודה ", ואלה מודגשות למעלה. שורות אלה מודיעות לנו אם למשתנים העצמאיים שלנו (שורות "מין" ו"דיפלומה ") והאינטראקציה שלהם (שורה" תעודת מין ") יש השפעה מובהקת סטטיסטית על המשתנה התלוי," עניין בפוליטיקה ". חשוב לבדוק תחילה את האינטראקציה "מין * תעודה" מכיוון שזה יקבע כיצד תוכל לפרש את התוצאות שלך (עיין במדריך המשופר שלנו למידע נוסף). אתה יכול לראות מה"סיג ". העמודה שיש לנו אינטראקציה מובהקת סטטיסטית ברמה p = .000. יתכן שתרצה לדווח על תוצאות "מין" ו"דיפלומה ", אך שוב, אלה צריכים להתפרש בהקשר של תוצאת האינטראקציה. אנו רואים מהטבלה למעלה כי לא היה הבדל מובהק סטטיסטית בעניין הממוצע בפוליטיקה בין גברים ונשים (p = 0.000), אך היו הבדלים מובהקים סטטיסטית בין רמות השכלה (p <.0005).

בדיקות פוסט הוק - אפקטים עיקריים פשוטים בסטטיסטיקה של SPSS

כאשר יש לך אינטראקציה משמעותית סטטיסטית, דיווח על ההשפעות העיקריות עלול להטעות. לכן עליכם לדווח על האפקטים העיקריים הפשוטים. בדוגמה שלנו, זה כרוך בקביעת ההבדל הממוצע בעניין בפוליטיקה בין מגדרים בכל דרג חינוכי, כמו גם בין רמת השכלה לכל מגדר. לרוע המזל, סטטיסטיקה של SPSS אינה מאפשרת לך לעשות זאת באמצעות הממשק הגרפי שאתה מכיר, אך מחייבת אותך להשתמש בתחביר. לכן, במדריך ה- ANOVA המשוכלל שלנו, אנו מראים לכם את ההליך לעשות זאת בסטטיסטיקה של SPSS, כמו גם להסביר כיצד לפרש ולכתוב את הפלט מהאפקטים העיקריים הפשוטים שלכם.

כאשר אין לך אינטראקציה משמעותית סטטיסטית, אנו מסבירים שתי אפשרויות העומדות בפניך, כמו גם נוהל שתוכל להשתמש בו בסטטיסטיקה של SPSS כדי להתמודד עם סוגיה זו.

טבלת השוואות מרובות

אם אין לך אינטראקציה מובהקת סטטיסטית, אתה עלול לפרש את תוצאות הבדיקה פוסט-הוק של Tukey עבור דרגות השכלה שונות, אשר ניתן למצוא בטבלת ההשוואות המרובות, כמוצג להלן:

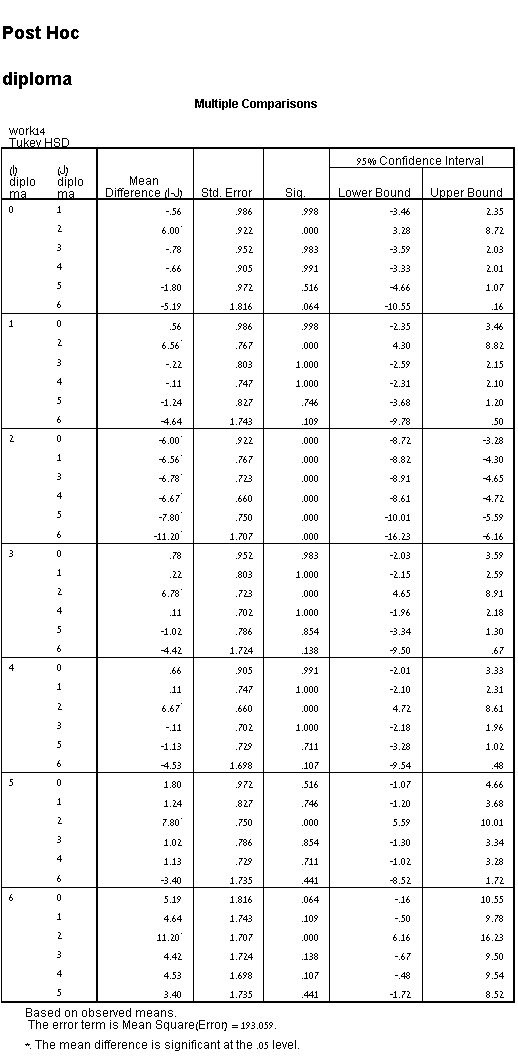
ניתן לראות מהטבלה למעלה שיש חזרה מסוימת על התוצאות, אך ללא קשר לאיזו שורה אנו בוחרים לקרוא, אנו מעוניינים בהבדלים בין (1) בית ספר ומכללה, (2) בית ספר ואוניברסיטה, ו ( 3) המכללה והאוניברסיטה. מהתוצאות ניתן לראות כי קיים הבדל מובהק סטטיסטית בין שלוש רמות ההשכלה השונות (p <.0005).

{ניתוח סטטיסטי}