רגרסיה לינארית

ניתוח רגרסיה לינארית באמצעות SPSS

מבוא

רגרסיה לינארית היא השלב הבא לאחר המתאם. הוא משמש כאשר אנו רוצים לחזות את ערכו של משתנה על סמך ערכו של משתנה אחר. המשתנה שאנחנו רוצים לחזות נקרא המשתנה התלוי (או לפעמים משתנה התוצאה). המשתנה בו אנו משתמשים כדי לחזות את ערכו של המשתנה האחר נקרא המשתנה הבלתי תלוי (או לעיתים משתנה החיזוי). לדוגמה, אתה יכול להשתמש ברגרסיה לינארית כדי להבין אם ניתן לחזות ביצועי בחינה על סמך זמן העדכון; האם ניתן לחזות צריכת סיגריות על בסיס משך העישון; וכן הלאה. אם יש לך שני משתנים או יותר תלויים, ולא רק אחד, עליך להשתמש ברגרסיה מרובה.

מדריך "התחלה מהירה" זו מראה לך כיצד לבצע רגרסיה לינארית באמצעות סטטיסטיקה של SPSS, וכן לפרש ולדווח על התוצאות ממבחן זה. עם זאת, לפני שנכיר לכם את הנוהל הזה, עליכם להבין את ההנחות השונות שעליהן הנתונים שלכם לעמוד בהן כדי שהרגרסיה הליניארית תתן לכם תוצאה תקפה. בהמשך נדון בהנחות אלה.

הנחות

כשאתה בוחר לנתח את הנתונים שלך באמצעות רגרסיה לינארית, חלק מהתהליך כרוך בבדיקה כדי לוודא שניתן לנתח את הנתונים שאתה רוצה לנתח באמצעות רגרסיה לינארית. עליכם לעשות זאת מכיוון שנכון להשתמש רק ברגרסיה לינארית אם הנתונים שלכם “עוברים” שש הנחות הנדרשות לצורך רגרסיה לינארית בכדי לתת לכם תוצאה תקפה. בפועל, בדיקת שש ההנחות הללו רק מוסיפה קצת יותר זמן לניתוח שלך, ומחייבת לך ללחוץ על עוד כמה כפתורים בסטטיסטיקה של SPSS בעת ביצוע הניתוח שלך, כמו גם לחשוב קצת יותר על הנתונים שלך, אבל זה משימה לא קשה.

לפני שנכיר לך את שש ההנחות הללו, אל תתפלא אם בניתוח הנתונים שלך בעצמך תוך שימוש בסטטיסטיקה של SPSS, הפרה אחת או יותר מההנחות הללו (כלומר, לא התקיימה). זה לא נדיר כאשר עובדים עם נתונים בעולם האמיתי ולא עם דוגמאות לספרי לימוד, שלרוב רק מראים לכם כיצד לבצע רגרסיה לינארית כשהכל מסתדר! עם זאת, אל תדאג. גם כאשר הנתונים שלך נכשלים בהנחות מסוימות, לעתים קרובות יש פיתרון להתגבר על זה. ראשית, נסתכל על שש ההנחות הללו:

* הנחה מס '1: יש למדוד את שני המשתנים שלך ברמה הרציפה (כלומר, הם משתני מרווח או יחס). דוגמאות למשתנים רציפים כוללים זמן עדכון (נמדד בשעות), אינטליגנציה (נמדדת באמצעות ציון מנת משכל), ביצועי הבחינה (נמדד מ -0 ל -100), משקל (נמדד בק"ג) וכן הלאה.

* הנחה מס '2: צריך להיות קשר ליניארי בין שני המשתנים. אמנם ישנן מספר דרכים לבדוק אם קיים קשר ליניארי בין שני המשתנים שלך, אך אנו מציעים ליצור מגרש פיזור באמצעות SPSS סטטיסטיקות בו אתה יכול לשרטט את המשתנה התלוי כנגד המשתנה הבלתי תלוי שלך ואז לבדוק באופן ויזואלי את הפיזור כדי לבדוק אם יש ליניאריות. המגרש שלך עשוי להיראות כמו אחד מהדברים הבאים:

אם הקשר המוצג במגרש הפיזור שלכם אינו לינארי, יהיה עליכם לבצע ניתוח רגרסיה לא ליניארי, לבצע רגרסיה פולינומית או “לשנות” את הנתונים שלכם, שתוכלו לעשות באמצעות SPSS Statistics. במדריך המשופר שלנו אנו מראים לך כיצד: (א) ליצור מגרש פיזור לבדיקת לינאריות בעת ביצוע רגרסיה לינארית באמצעות סטטיסטיקה של SPSS; (ב) לפרש תוצאות מפוזרות שונות; ו (ג) לשנות את הנתונים שלך באמצעות נתונים סטטיסטיים של SPSS אם אין קשר ליניארי בין שני המשתנים שלך.

הנחה מס '3: לא אמורים להיות מתארים משמעותיים. מקדם מתח הוא נקודת נתונים נצפתה שיש לה ערך משתנה תלוי השונה מאוד לערך שחזוי משוואת הרגרסיה. מכיוון שכך, מחליף יהיה נקודה על מגרש פיזור שנמצא (אנכית) הרחק מקו הרגרסיה המציין שיש לו שארית גדולה, כפי שהודגש להלן:

הבעיה עם המממנים היא שהם יכולים להשפיע לרעה על ניתוח הרגרסיה (למשל, להפחית את ההתאמה של משוואת הרגרסיה) המשמשת לחיזוי הערך של המשתנה התלוי (התוצאה) על בסיס המשתנה הבלתי תלוי (מנבא). זה ישנה את התפוקה שמייצרת סטטיסטיקה של SPSS ותפחית את הדיוק החזוי של התוצאות שלך. למרבה המזל, כשאתה משתמש בסטטיסטיקה של SPSS כדי להריץ רגרסיה לינארית על הנתונים שלך, אתה יכול לכלול בקלות קריטריונים שיעזרו לך לאתר מחיצות אפשריות. במדריך הרגרסיה הליניארית המשופרת שלנו, אנו: (א) מראים לך כיצד לאתר מחיצות באמצעות "אבחון casewise", שהוא תהליך פשוט בעת השימוש בסטטיסטיקה של SPSS; ו (ב) לדון בכמה מהאפשרויות העומדות בפניך כדי להתמודד עם מתחרים.

הנחה מס '4: עליכם להיות עצמאים של תצפיות, אותן תוכלו לבדוק בקלות באמצעות נתון Durbin-Watson, שהוא מבחן פשוט להפעלה באמצעות סטטיסטיקה של SPSS. אנו מסבירים כיצד לפרש את התוצאה של נתון דורבין-ווטסון במדריך הרגרסיה הליניארי המשופר שלנו.

הנחה מס '5: הנתונים שלך צריכים להראות הומוצססטיות, וכאן השונות לאורך הקו המתאים ביותר נותרות דומות כשאתה נע לאורך הקו. בעוד אנו מסבירים יותר מה המשמעות של זה וכיצד להעריך את ההומוסססטסטיות של הנתונים שלך במדריך הרגרסיה הליניארית המשופרת שלנו, התבונן בשלושת המפזרים למטה, המספקים שלוש דוגמאות פשוטות: שניים של נתונים שלא מצליחים את ההנחה (המכונה הטרוסצסטיות) ואחד מהנתונים העונים על ההנחה הזו (נקרא homoscedasticity):

אמנם אלה עוזרים להמחיש את ההבדלים בנתונים העונים או מפרים את ההנחה של הומוסצסטיות, נתונים בעולם האמיתי יכולים להיות הרבה יותר מבולגנים ולהמחיש דפוסים שונים של הטרוססטסטיות. לפיכך, במדריך הרגרסיה הליניארית המשופרת שלנו אנו מסבירים: (א) כמה מהדברים שתצטרך לקחת בחשבון בעת פירוש הנתונים שלך; ו (ב) דרכים אפשריות להמשיך בניתוח שלך אם הנתונים שלך לא עומדים בהנחה זו.

הנחה מס '6: לבסוף, עליכם לבדוק שהשאריות (שגיאות) של קו הרגרסיה מופצות באופן רגיל (אנו מסבירים מונחים אלה במדריך הרגרסיה הליניארי המשופר שלנו). שתי שיטות נפוצות לבדיקת הנחה זו כוללות שימוש בהיסטוגרמה (עם עקומה נורמלית המופעלת על-גבי הצגה) או עלילת P-P רגילה. שוב, במדריך הרגרסיה הליניארית המשופרת שלנו, אנו: (א) מראים לך כיצד לבדוק הנחה זו באמצעות סטטיסטיקה של SPSS, בין אם אתה משתמש בהיסטוגרמה (עם עקומה נורמלית המועברת) או עלילת P-P רגילה; (ב) להסביר כיצד לפרש דיאגרמות אלה; ו- (ג) לספק פיתרון אפשרי אם הנתונים שלך לא עומדים בהנחה זו.

אתה יכול לבדוק את ההנחות מס '2, # 3, # 4, # 5 ו- # 6 באמצעות נתונים סטטיסטיים של SPSS. יש לבדוק תחילה את ההנחות מס '2, לפני שעוברים להנחות מס' 3, # 4, # 5 ו- # 6. אנו ממליצים לבחון את ההנחות בסדר הזה מכיוון שההנחות מס '3, # 4, # 5 ו- # 6 מחייבות להפעיל תחילה את הליך הרגרסיה הליניארית בסטטיסטיקה של SPSS, כך שקל יותר להתמודד עם אלה לאחר בדיקת ההנחה מס' 2. רק זכרו שאם לא מבצעים נכון את הבדיקות הסטטיסטיות בהנחות אלה, יתכן שהתוצאות שתקבלו בעת ביצוע רגרסיה לינארית אינן תקפות. זו הסיבה שאנחנו מקדישים מספר חלקים במדריך הרגרסיה הליניארי המשופר שלנו כדי לעזור לך להשיג את זה נכון. תוכלו ללמוד יותר על התוכן המשופר שלנו בכללותו בדף התכונות שלנו: סקירה כללית, או ליתר דיוק, ללמוד כיצד אנו עוזרים בבדיקת הנחות בדף התכונות שלנו: הנחות.

איך מריצים רגרסיה לינארית ב-SPSS

לצורך הדוגמה והתרגות הורידו את הקובץ הבא:
קובץ תרגול להורדה

בקובץ קיימים נתונים דמוגרפים רבים שיעזרו לנו לעשות ניתוחים סטטיסטיים שונים, נתמקד כרגע בהרצת רגרסיה לינארית

מדריך רגרסיה לינארית ב-SPSS

תפתחו את הקובץ SPSS ולחצו:

Analyze > Regression > Linear

יפתח חלון הבא:

בחלון שנפתח יש לבחור משתנה תלוי ובלחיצה על כפתור להכניס אותו לרגרסיה לאחר מכן יש לבחור משתנים המסבירים ובלחיצה על כפתור להכניסם לרגרסיה גם. לצורך הדוגמה בחרנו במשתנה תלוי (מוסבר) שכר ומשתנים בילתי תלויים (מסבירים) גיל מין ושנות לימוד. לאחר בחירת המשתנים יש ללחוצ על כפתור

הסבר של פלט SPSS - רגרסיה לינארית

הצהרה על הבעיה

טבלת Model Summary

טבלה זו מציגה את ערכי R ו- R2. ערך R מייצג את המתאם הפשוט והוא 0.395 (העמודה "R"), מה שמצביע על דרגה גבוהה של מתאם. ערך ה- R2 (העמודה "ריבוע R") מצביע על כמה מהשונות הכוללת במשתנה התלוי, מחיר, ניתן להסביר על ידי המשתנה הבלתי תלוי, הכנסה. במקרה זה ניתן להסביר 15.6% שזה נמוך מאוד.

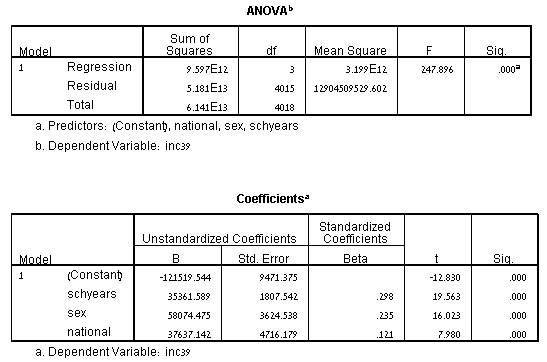
טבלת ANOVA

הטבלה הבאה היא טבלת ANOVA, המדווחת עד כמה משוואת הרגרסיה מתאימה לנתונים (כלומר, חוזה את המשתנה התלוי) והיא מוצגת להלן:

טבלה זו מצביעה על כך שמודל הרגרסיה מנבא היטב את המשתנה התלוי. כיצד אנו יודעים זאת? התבונן בשורת "רגרסיה" ועבור ל"סיג ". טור. זה מצביע על המשמעות הסטטיסטית של מודל הרגרסיה שהופעל. כאן, p <0.0005, שהוא פחות מ- 0.05, ומציין כי בסך הכל, מודל הרגרסיה מנבא באופן סטטיסטי את משתנה התוצאה (כלומר, הוא מתאים להתאים).

טבלת Coefficients

טבלת מקדמים מספקת לנו את המידע הדרוש כדי לחזות את המחיר מההכנסה, כמו גם לקבוע אם ההכנסה תורמת באופן סטטיסטי למודל (על ידי התבוננות בעמודה "סיג."). יתר על כן, אנו יכולים להשתמש בערכים בעמודה "B" בעמודה "מקדמים לא סטנדרטיים", כמוצג להלן:

להציג את משוואת הרגרסיה כ:

wage=-121519+35361(schyears)+58074(sex)+37637(national)

במילים אחרות כל שנת לימוד מוסיפה 35361 ש'ח גבר מרוויח 58074 ש'ח יותר מאשה ויהודים מרוויחים 37637 ש'ח יותר מאחרים. ניתן לראות כי כל התוצאות מובהקות (sig=0.000)
החותך עם הציר y הינו -121519

{ניתוח סטטיסטי}